Informatiker Board | formale Sprachen | Reguläre Sprache - Pumping Lemma

Informatiker Board » Themengebiete » Theoretische Informatik » formale Sprachen » Reguläre Sprache - Pumping Lemma » Antwort erstellen

» Hallo Gast [Anmelden|Registrieren]

Antwort erstellen

Benutzername:

(du bist nicht eingeloggt!)

Thema:

Nachricht:

HTML ist nicht erlaubt
BBCode ist erlaubt
Smilies sind erlaubt
Bilder sind erlaubt

Smilies: 21 von 33

einfacher Modus erweiterter Modus

aktuellen Tag schließen

alle Tags schließen

Spamschutz:
Text aus Bild eingeben

URLs automatisch umwandeln: fügt automatisch [url] und [/url] in Internet-Adressen ein.
Smilies in diesem Beitrag deaktivieren.
BBCode in diesem Beitrag deaktivieren.
Bilder in diesem Beitrag deaktivieren.
Signatur anzeigen: Soll die im Profil eingestellte Signatur an den Beitrag angehangen werden?
Nachrichtenlänge überprüfen

Die letzten 10 Beiträge

3c7

Hi, ich hoffe das ist so verständlich:

Du kannst also auch abpumpen (i=0 setzen), was hier sinnvoller ist. So kannst du relativ schnell zeigen, dass die Sprache nicht regulär ist.

Gruß 3c7

Laura94

Hey interessanter Beitrag, leider komme ich mit dem Pumping-Lemma allgemein garnicht klar.

Habe heut meine Klausur geschrieben und man sollte zeigen, dass folgende Sprache nicht regulär ist:

L={ a^s b^u | s > u}

Wenn ich jetzt n=u setze, dann ist jedes Wort x länger als 2*n. Da |uv|<n sein muss, kann v also nur aus a's bestehen. Wenn ich das Wort dann aufpumpe ist uv^iw immer noch in der Sprache, weil ich ja nur mehr a's hinzufüge.

Ich fürchte fast, es hat was mit der Wahl meines "n" zu tun, aber rein von der Logik her, kann ich für jedes n ja einfach Zerlegung finden in der v=a ist. Und das kann ich ja beliebig aufpumpen.

Die Klausur ist zwar eh gelaufen, aber vllt kann mir jemand sagen, wie man das richtig gelöst hätte Augenzwinkern

Grüße

3c7

Hallo zusammen,

hab gerade ein ähnliches Problem. Eine meiner Meinung nach reguläre Sprache L = {(a^k)^2 | k>=0} lässt sich mit Hilfe einer Typ 3 Grammatik G=({a}, {S,A} {S->e | aA, A-> aS}, S) erstellen. Beispiele für in L enthaltene Wörter wären also L = {e, aa, aaaa, aaaaaa, ...}.

Wende ich nun das Pumping Lemma auf L an, komme ich schlussendlich auf einen Widerspruch.
Ich habe mal versucht, mein Vorgehen aufzuschreiben:

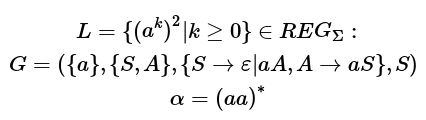
Ich vermute, der Fehler liegt in der Schlussfolgerung, beziehe mich ja nur auf die Länge des Wortes. Kann mir da jemand helfen?

Viele Grüße

Edit:
Andere Überlegung. Nach dem Pumping Lemma liegt die Länge von x zwischen zwei Quadraten und daher gehört x nicht in die Sprache:

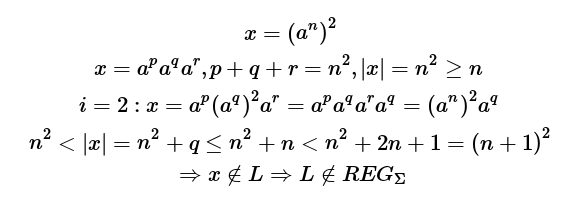
Andere Argumentation, gleiches Ergebnis. Da ist doch irgendwo ein gewaltiger Denkfehler drin...

Edit 2:
Zur Ursprungsthematik:
Ich gehe davon aus, das bei Sprachen mit endlicher Anzahl Wörter das Pumping Lemma nicht anwendbar ist. Wir haben bei uns in der Hochschule darüber gesprochen, dass die Variable für die Länge des gewählten Wortes - in diesem Fall n - quasi "unbekannt" ist. Man sagt nur, dass $[latex]\exists n \in \mathbb N[/latex]$ und ab der Länge des Wortes $[latex]|x| \ge n[/latex]$ eine Zerlegung [latex]x=uvw[/latex]

existiert.

Karlito

Auf jeden Fall ist es so, dass jede Sprache, welche nur endlich viele Elemente hat, regulär ist. Wie Du schon sagst, braucht man ja nur jedes Wort mit | in einem regulären Ausdruck zu verbinden. Somit gibt es einen regulären Ausdruck, welcher die Sprache akzeptiert und das genügt meist als Nachweis, dass die Sprache regulär ist. Alternativ kann man auch für jedes Wort einen endlichen Automaten konstruieren. Somit ist bewiesen, dass jedes Wort regulär ist. Die gesamte Sprache ist dann die Vereinigung aller dieser Wörter. Dazu konstruiert man einen neuen Automaten, indem man einen neuen Startzustand einführt und einen epsilon-Übergang zu den Startzuständen der Automaten der einzelnen Wörter.

Mir gefällt die Formulierung des Pumping Lemmas jedoch nicht, da es intuitiv erst einmal keine Aussage darüber gibt, wie das n zu gestalten ist. Das würde ich gern noch einmal hinterfragen. Ich denke, dass die Formulierung schon logisch durchdacht ist, aber ein quäntchen Verständnis fehlt. Die Theoretiker sind da sicher ein wenig fitter... Diejenigen, die ich bisher gefragt habe, waren durchweg eher Softwaretechnologen.

Gruß,

Karlito

Laura94

Danke nochmal, ich denke mit dem n könntest du durchaus Recht haben.

Wobei ich mir grad überlege, ob nicht jede Sprache mit einer endlichen Menge an Wörtern regulär ist.
Man kann ja für jede Sprache, die aus einer endlichen Menge an Wörtern besteht einen regulären Ausdruck finden, indem man einfach alle Wörter mit dem |-Operator verknüpft.

Dann müsste die Zerlegung nach dem Pumping-Lemma ja nur für abzählbar-unendliche Sprachen möglich sein, da man beim pumpen sonst irgendwann "zu lang" werden würde.

Karlito

Ich habe jetzt schon mit 2 Studenten und einem Lehrstuhlmitarbeiter diskutiert. Bisher kein 100%iger Konsens. Meine Vermutung ist, dass man das n für die Mindestlänge einfach größer setzt als das längste Wort. Dann gibt es keine Wörter, welche länger sind als n und somit ist auch die Zerlegung hinfällig. Das wird so nicht aus der Formulierung klar, aber ich sehe als einzige logische Argumentation.

Ich frage bei Gelegenheit noch eine Bekannte, welche bei den Theoretikern arbeitet um das abzusichern.

Gruß,

Karlito

Laura94

Zitat:

Original von Lena95
Vielen Dank smile

Ups, obige Antwort kommt natürlich von mir, ich hatte versucht mich mit einem Matheboard Account anzumelden, da ich dachte die Foren würden vllt irgendwie "zusammenhängen".

Jetzt sollte ich richtig registriert sein smile

Lena95

Vielen Dank smile

Karlito

Genau das Problem hatte ich auch immer und habe es immer ignoriert. Ich werde mal versuche es zeitnah herauszufinden und hier zu posten.

Gruß,

Karlito

Laura94

Reguläre Sprache - Pumping Lemma

Meine Frage:
Hey, ich beschäftige mich grade mit dem Pumping-Lemma, muss aber gestehen, dass es mir ziemlich schwer fällt, es zu verstehen.

Reguläre Sprachen wurden bei uns in der Vorlesung über die Chomsky-Hierarchie definiert, also:

Typ 3 ("regulär")
Für alle Regeln w1 -> w2 gilt:
w1 ist eine einzelne Variable ( $[latex]w1 \in V[/latex]$ )
$[latex]w2 \in E \bigcup EV[/latex]$ (rechte Seite ist einzelnes Terminalzeichen oder ein Terminalzeichen gefolgt von einer Variablen.

Meine Ideen:
Wenn ich dann also ein Grammatik hätte zB:
G = ({S}, {a}, P, S)
mit P={
S->a
}

Dann entspräche das meinem Verständnis nach einer Grammatik für eine Typ3-Sprache, also einer regulären Sprache.
Eben die Sprache, die als Wort nur das a enthält.

Wenn ich letzte eine Zerlegung nach dem Pumping-Lemma suche, dann gibt es ja nur eine mögliche Zerlegung für:
x=uvw. Nämlich v=a mit n=1.

Demnach müsste ich das v ja jetzt aufpumpem können, und das Wort müsste immer noch in der Sprache liegen.

Für alle i aus der natürlichen Zahlen mit 0, gilt das das "aufgepumpte Wort" für i=0 und für alle i>=2 kein Wort der Sprache ist.
Somit müsste die Sprache ja nicht regulär sein.

Also irgendwo muss da ja ein Denkfehler drin sein, da die Sprache ja laut Definition eine reguläre Sprache sein sollte.

Hoffe jemand kann mir da weiterhelfen.

Grüße